Invited speakers:

Gergő Nemes (Harbin Institute of Technology) 

Minjie Luo (Donghua University) 

Organizers: Lun Zhang & TaiyangXu

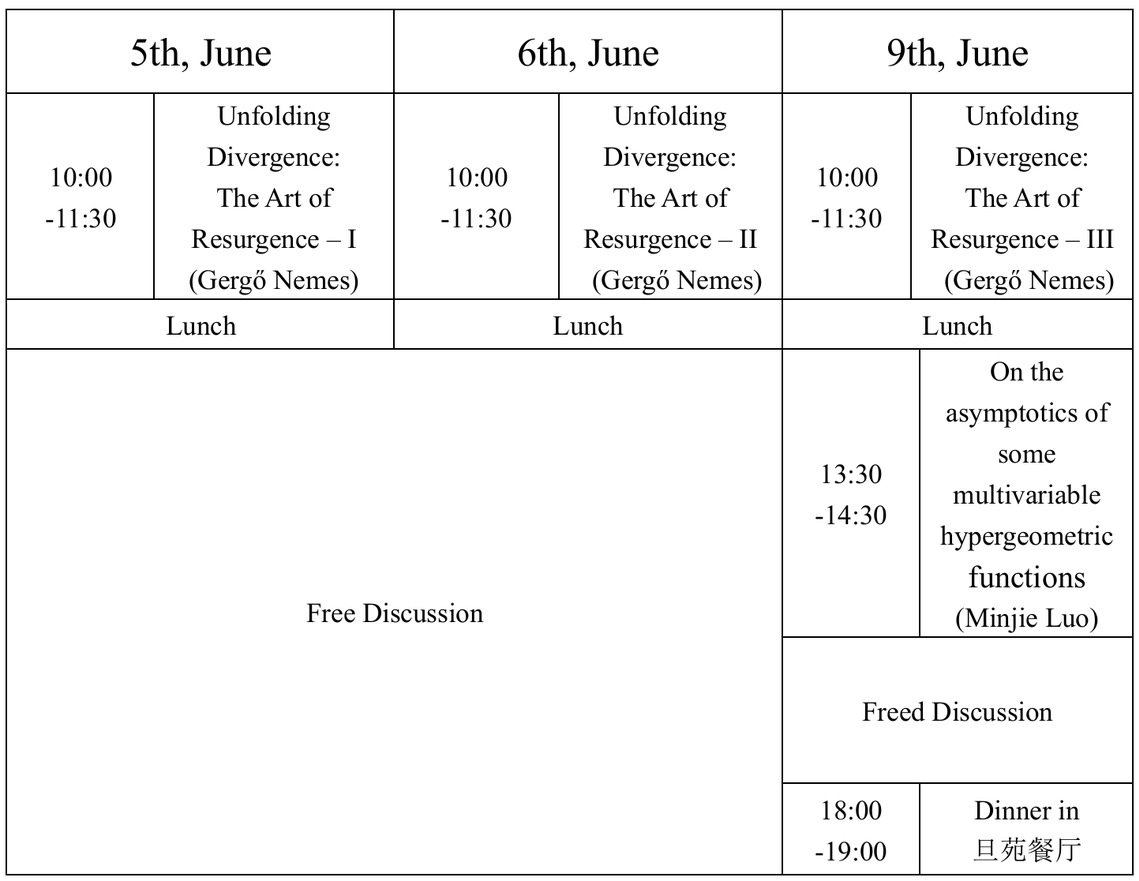
Lecture: Unfolding Divergence: The Art of Resurgence

Speaker: Gergő Nemes

Abstract: Asymptotic expansions have long been seen as formal tools for approximation, but they hide a deep analytic structure behind their divergent nature. This lecture series takes you on a journey through the theory and applications of resurgence, starting with the history of asymptotics and Stokes’key ideas. We then look at the important work of Dingle, Écalle, and Berry, which led to the modern understanding of asymptotic expansions. The series covers hyperasymptotic methods for integrals with saddle points and shows how resurgence appears in both linear and nonlinear differential equations, in parameter-dependent expansions, and in transitional regions. The series ends with a study of resurgence in implicit functions and the higher-order Stokes phenomenon.

About the speaker: Gergő Nemes is a Professor in the School of Mathematics at the Harbin Institute of Technology, China. He obtained a B.Sc. in mathematics (with distinction) and a M.Sc. in mathematics (with honours) from Loránd Eötvös University, Budapest, Hungary and a Ph.D. in mathematics from Central European University in Budapest, Hungary. Nemes has research interests in asymptotic analysis, Écalle theory, exact WKB analysis, and special functions.

Talk: On the asymptotics of some multivariable hypergeometric functions

Speaker: Minjie Luo

Abstract: In a series of papers published between 1954 and 1957, S. Saran systematically studied the hypergeometric functions of three variables. In this talk, we present the latest results on the asymptotics of Saran’s $F_K$ function and its related functions. A brief introduction to the history and applications of these multivariable hypergeometric functions is also provided to offer inspiration and insights for further research. In addition, we suggest some promising future research directions.

About the speaker: Dr. Min-Jie Luo is currently working as an Associate Professor in the Department of Mathematics at Donghua University, Shanghai, China. He received his PhD from East China Normal University, China, and completed his postdoctoral research at City University of Hong Kong, China. He has published more than 20 research papers in journals of international repute. His research interests are Special Functions and Fractional Calculus.